题目描述

众所周知，小凯是一个网瘾少年，这天梦里，他又梦到了自己在玩一款游戏——

在一张 $n×m$ 大小的地牢里（左下角为 $(1,1)$ ，右上角为 $(n,m)$ ），有 $K$ 个怪物，小凯操控着主角为了获取收益来进入地牢猎杀这些怪物。

对于每个怪物有这样三个属性，价值 $A_i$ ，攻击力 $B_i$ ，攻击距离 $C_i$ 。

主角的初始生命值为 $1$，在进入地牢前，你会有一个商店供你购买生命值，你可以贷款 $x$ 个金币（ $x$ 为任意正整数）来获得 $x$ 点生命值，当然你也可以选择不贷款。注意你只能在进入地牢前购买生命值，进入地牢后将无法购买生命值。

一开始，主角会出现在地图的 $(sx,sy)$ 位置，保证该位置上没有怪物。

在每回合的开始，主角可以进行下面两个操作中的一个操作。

1. 离开地牢，获得当前击杀怪物的金币并进行结算。

2. 瞬移到同行/同列上与当前位置距离不超过 $d$ 的没有怪物的地图内的位置，并且消灭瞬移起点和终点相连的线段上的所有怪物。（消灭怪物可以瞬间获得怪物的价值数量的金币）这里的距离可以用曼哈顿距离来理解。

在每回合结束时，会结算怪物对主角造成的伤害。（死亡的怪物不会对主角造成伤害）

对于每个怪物而言，如果主角和怪物之间的曼哈顿距离小于等于怪物的攻击距离 $C_i$ ，那么主角就会受到 $B_i$ 点伤害。在任意时刻主角的生命值小于等于 $0$ 角色就会死亡，并且失去所有获得的金币。

试问主角最多能获得多少金币。（最后收益为击杀怪物获得金币减去一开始贷款购买的生命值的花费）

曼哈顿距离的定义如下，对于点 $S(x_1,y_1)$ 和点 $T(x_2,y_2)$ ，他们的曼哈顿距离为 $|x_1−x_2|+|y_1−y_2|$

输入格式

第一行有一个整数，$T (1≤T≤15)$ ，代表数组组数

每组数据第一行有三个整数， $n,m,K$， $(2≤n,m≤30,1≤K≤10)$

第二行是一个整数，$d$ （$1≤d≤8$），代表瞬移的距离上限

接下来有 $K$ 行，每行有五个整数 $X_i,Y_i,A_i,B_i,C_i$ 。其中 $X_i,Y_i$ 表示怪物现在所在点 $(X_i,Y_i)$ , $A_i,B_i,C_i$分别表示怪物 $i$ 的价值、攻击力和攻击距离。（$1≤X_i≤n,1≤Y_i≤m,1≤A_i,B_i≤10^4,1≤C_i≤8$）

最后一行两个整数 $sx,sy$ 表示主角一开始在的位置。（$1≤sx≤n,1≤sy≤m$）

输出格式

对于每组数据输出一行一个整数代表最多可以获得的收益。

输入样例

1
4 5 2
3
1 4 4 3 2
4 4 7 2 3
1 5

输出样例

9

提示

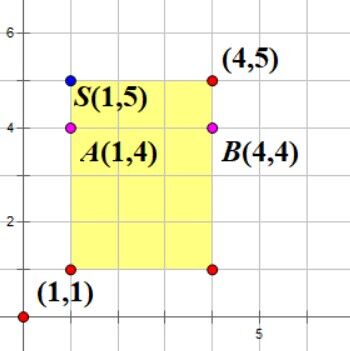
对于样例 $1$ 而言，其中一种最优策略如下：

我们一开始贷款 $2$ ，让主角在进入地牢前生命值达到 $3$。

$1$：主角一开始在 $S(1,5)$ ，我们可以先瞬移到 $(1,2)$ ，解决掉 $(1,4)$ 所在的敌人，获得 $4$ 枚金币

此时场上只剩下在点 $(4,4)$ 的怪物，因为 $(1,2)$ 和 $(4,4)$ 的曼哈顿距离为 $5$，所以主角不会受到伤害

$2$：主角从 $(1,2)$ 瞬移到 $(4,2)$

因为 $(4,2)$ 和 $(4,4)$ 的曼哈顿距离为 $2$，小于怪物 $2$ 的攻击距离 $3$，所以主角会受到 $2$ 点伤害

$3$：主角从 $(4,2)$ 瞬移到 $(4,5)$ ，解决掉 $(4,4)$ 所在的敌人，获得 $7$ 枚金币

没有怪物存在场上，所以主角不会受到伤害

$4$：离开地牢，结算收益

我们最后的答案就是 $-2+4+7=9$。